Rotation about X
\(\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & cos\theta & -sin\theta & 0 \\
0 & sin\theta & cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\)
Rotation about Y
\(\begin{bmatrix}
cos\theta & 0 & -sin\theta & 0 \\
0 & 1 & 0 & 0 \\
sin\theta & 0 & cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\)
Rotation about Z
\(\begin{bmatrix}
cos\theta & -sin\theta & 0 & 0 \\
sin\theta & cos\theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\)
Explanation
The rotation matrix is perhaps the least intuitive of the four matrix types. Combining sin and cos with x and y, flipping signs in an apparently arbitrary manner is, well, weird..
Starting with a vertex P that we want to rotate about the origin by an angle \(\theta\):
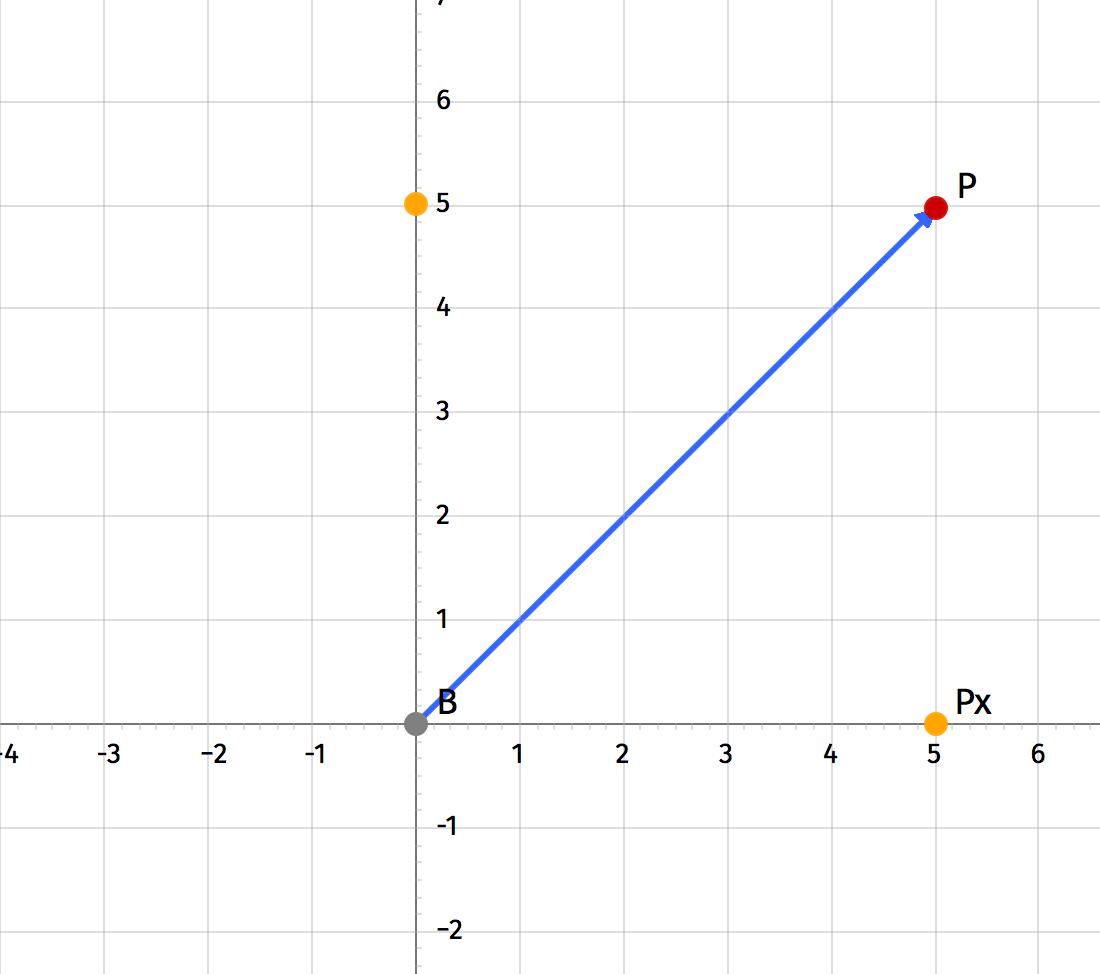
We can see that the point P can be expressed as the sum of two vectors from the origin, laying along the X and Y axis:
\(
\vec{P_x} = P * \hat{x} \\
\text{ and } \\
\vec{P_y} = P * \hat{y} \\
\).
Solving half the problem
Now, rotating an arbitrary point is a difficult problem. However, rotating a point that lay on an axis – that is, a point which has only one non-zero value, is pretty simple. Since we can split any vector into a sum of its basis vectors multiplied by its magnitude, we can split this process into a few parts:
- Define two vectors which are zero, except for the part that lay on an axis. You’ll need one of these for each axis, except for the axis about which we are rotating. When rotating a 3D point about the Z axis, we’ll get \(\vec{x} = (x,0,0)\) and \(\vec{y} = (0,y,0)\).
- For \(\vec{x}\),
- Define a right triangle with a hypotenuse of length X, and an angle θ relative to the X axis.
- Calculate the length of the legs of that triangle in terms of X and θ
- For \(\vec{y}\),
- Define a right triangle with a hypotenuse of length Y, and an angle θ relative to the Y axis.
- Calculate the length of the legs of that triangle in terms of Y and θ
So, let’s try rotating \(\vec{P}_x\), which is a vector from the origin to the projection of \(\vec{P}\) on to the X axis.
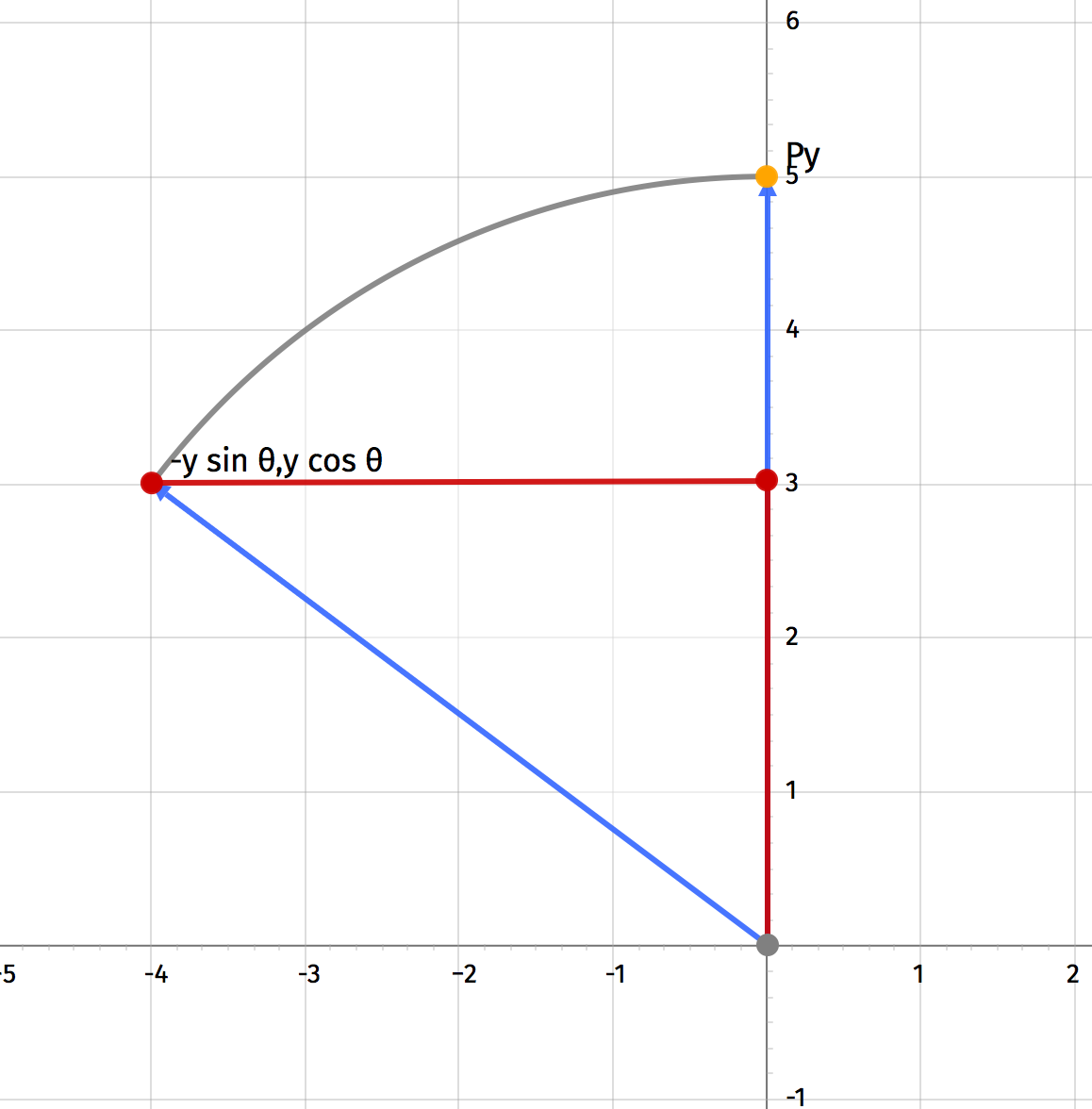
In English: if the point that we want to rotate, P, is (5,3), then \(\vec{P}_x\) is the vector (5,0). Just take the X component of the original point and set everything else to zero. By contrast, the Y component vector \(\vec{P}_y\) would be (0,3).
The vector from the origin to the point \(\vec{x}^1\) (pronounced “x prime”) is just the corner of a right triangle, the same distance from the origin as \(\vec{x}\), forming angle \(\angle\theta\) with the \(\hat{X}\) axis:
Now, we just have a right triangle with hypotenuse length x, angle \(\angle\theta\) with the X axis. Basic trigonometry tells us that the legs of the triangle are \(x \cos \theta\) and \(x \sin \theta\).
We can express that new point as a sum of two vectors by multiplying by the unit vectors (basis vectors) of the X and Y axis:
\(\vec{{P_x}^{new}} = \vec{x}\cos\theta * \hat{x} + \vec{x}\sin\theta * \hat{y}\)This gives us the rotated vector \(\vec{x}\) from our original point.
Now, we need to repeat that for the Y component.
The math is identical, except in this case, the Y component moves left and down(to keep with our counter-clockwise (“ccw”) rotation convention we’ve used for the X component).
For angles less than 180 degrees, the rotated Y component will wind up on the left side of the Y axis. The angle θ in this case is relative to the positive Y axis. So, the new point will be at (\(-y \sin\theta\),\(y\cos\theta\)). This can be expressed as a vector addition by multiplying each component by a unit vector:
\(\vec{{P_y}^{new}} = -\vec{y}\sin\theta * \hat{x} + \vec{y}\cos\theta * \hat{y}\)Adding it up
Now, we have two vectors: \(\vec{{P_x}^{new}}\) and \(\vec{{P_y}^{new}}\). What we really want is the point \(\vec{P^{new}}\). Fortunately, we can express this as
\(\vec{P^{new}} = \vec{{P_x}^{new}} + \vec{{P_y}^{new}}\)Where:
\(\vec{{P_x}^{new}} = \vec{x}\cos\theta * \hat{x} + \vec{x}\sin\theta * \hat{y} \\
\vec{{P_y}^{new}} = -\vec{y}\sin\theta * \hat{x} + \vec{y}\cos\theta * \hat{y} \\
\)
Grouping like terms:
\(\vec{P^{new}} = \hat{x} * (\vec{x}\cos\theta -\vec{y}\sin\theta) + \hat{y} * (\vec{x}\sin\theta + \vec{y}\cos\theta) \\
\)
Or, as a 2×2 matrix operation:
\(\begin{bmatrix}
\vec{P^{new}}_x & \vec{P^{new}}_y \\
\end{bmatrix}
\text{=}
\begin{align}
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{bmatrix}
\begin{bmatrix}
\vec{P}_x \\
\vec{P}_y \\
\end{bmatrix}
\end{align}
\)
But, we like 4×4 matrices (because they let us add translation, which is impossible in 3D with a 3×3 or 2×2 matrix):
\(\vec{P^{new}} =
\begin{bmatrix}
x^{new} & y^{new} & z^{new} & w^{new} \\
\end{bmatrix}
\text{=}
\begin{align}
\begin{bmatrix}
\cos\theta & -\sin\theta & 0 & 0 \\
\sin\theta & \cos\theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
\vec{P}_x \\
\vec{P}_y \\
\vec{P}_z \\
\vec{P}_w \\
\end{bmatrix}
\end{align}
\)
Note that this leaves the z and w components unchanged.
In other planes
The operation is identical for rotations about Y and Z. Note, however, that the scalars must be moved to the correct cells:
| Rotation axis | X | Y | Z |
| X | + | + | |
| Y | + | + | |
| Z | + | + |
See the top of this page for examples.